The Foundation of Main Trigonometric Identities
Did you know that the most useful trigonometric identities stem from two fundamental trigonometric angle sum formulas?
From these formulas, you can derive three other types of trigonometric identities, each building foundation for the next ones, like a four-storey house!
Look through the “layers” of trigonometric identities and try to follow through the derivations step-by-step using the diagram below. Understanding the steps will help you recall the identities naturally and effortlessly.
Prerequisite: Try to see where the trigonometric angle sum identities for sin and cos come from using this geometric explanation. It is challenging, so don’t worry if you don’t get it right away. Just make sure that you understand that the formulas don’t come from thin air.
$$ \textbf{\textcolor{orange}{Layer 1: Angle Sum Identities}} \\ \begin{align*} \sin(\alpha + \beta) &= \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) \quad \text{(Mnemonic: sico + sico)} \\ \cos(\alpha + \beta) &= \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta) \quad \text{(Mnemonic: coco - sisi)} \\ \tan(\alpha + \beta) &= \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha)\tan(\beta)} \end{align*} $$To get from \(\textbf{\textcolor{orange}{Layer 1}}\) to \(\textbf{\textcolor{darkgreen}{Layer 2}}\), let \(\alpha = \beta = \theta\), turning the sum of angles \((\alpha + \beta)\) into a “double” angle \(2\theta\).
Substitute the new values of \(\theta\) into the angle sum identities to obtain the double angle identities.
* See Appendix 1 for the proof of tangent angle sum identity
$$ \textbf{\textcolor{darkgreen}{Layer 2: Double Angle Identities}} \\ \begin{align*} \sin(2\theta) &= 2\sin(\theta)\cos(\theta) \\ \cos(2\theta) &= \cos^2(\theta) - \sin^2(\theta) \\ \tan(2\theta) &= \frac{2\tan(\theta)}{1 - \tan^2(\theta)} \end{align*} $$This is the final form of the \(\sin\) and \(\tan\) double angle identities. But we can further transform the \(\cos(2\theta)\) double angle formula to get to the next layers.
To get from \(\textbf{\textcolor{darkgreen}{Layer 1}}\) to \(\textbf{\textcolor{pink}{Layer 3}}\), we will need to use the other two forms of the cosine double angle identity:
$$ \begin{align*} \cos(2\theta) &= \cos^2(\theta) - \sin^2(\theta) &= 2\cos^2(\theta) - 1 &= 1 - 2\sin^2(\theta) \end{align*} $$Consider the Pythagorean Identity \(1 = \sin^2(\theta) + \cos^2(\theta)\).
Move \(\sin^2(\theta)\) to the side of 1 to get \(\cos^2(\theta) = 1 - \sin^2(\theta)\). Now plug the \(\cos^2(\theta)\) into the double angle identity \(\cos(2\theta) = \cos^2(\theta) - \sin^2(\theta)\) to get \(\cos(2\theta) = 1 - 2\sin^2(\theta)\).
You can get \(\cos(2\theta) = 2\cos^2(\theta) - 1\) in an identical way.
Finally, we can get our new identities \(\cos(2\theta) = 2\cos^2(\theta) - 1\) and \(\cos(2\theta) = 1 - 2\sin^2(\theta)\) to get the power reduction identities by isolating \(\sin^2(\theta)\) (and \(\cos^2(\theta)\) respectively).
The \(\tan^2(\theta)\) is the ratio between the two identities.
$$ \textbf{\textcolor{pink}{Layer 3: Power Reduction Identities}} \\ \begin{align*} \sin^2(\theta) &= \frac{1 - \cos(2\theta)}{2} \\ \cos^2(\theta) &= \frac{1 + \cos(2\theta)}{2} \\ \tan^2(\theta) &= \frac{1 - \cos(2\theta)}{1 + \cos(2\theta)} \end{align*} $$Finally, to get from \(\textbf{\textcolor{pink}{Layer 3}}\) to \(\textbf{\textcolor{lightgreen}{Layer 4}}\), let \(\theta = \alpha/2\) (it doesn’t make intuitive sense to do this, but let’s try and see what happens).
This gives us \(\sin^2 (\alpha/2) = \frac{1 - \cos(\alpha)}{2}\) (analogous for \(\cos\))
The final step to get the half-angle identities is to take the square root of both sides to get \(\pm\sqrt{\frac{1 - \cos(\alpha)}{2}}\) and \(\pm\sqrt{\frac{1 + \cos(\alpha)}{2}}\).
The \(\pm\) depends on the quadrant in which \(\frac{\alpha}{2}\) falls. For example, for \( \frac{\alpha}{2} = \frac{\pi}{4}\) the value of \(sin\) will be positive since it is positive in first and second quadrants. The same holds for \(cos\), with the difference that it is positive in first and forth quadrants.
As always the ratio of the half angle formulas of \(\sin\) to \(\cos\), so the tangent half-angle formula is \(\tan(\alpha/2) = \sqrt{\frac{1-\cos(\alpha)}{1+\cos(\alpha)}}\)
This formula can further be developed into \(\frac{\sin(\alpha)}{1+\cos(\alpha)}\) and \(\frac{1-\cos(\alpha)}{\sin(\alpha)}\) by multiplying both sides of the equation by \(\sqrt{\frac{1 + \cos(\alpha)}{1+\cos(\alpha)}}\), which is a fancy way of writing 1.
On the left, \(\tan(\alpha/2)\) will remain unchanged, while on the right we can use difference of squares and the Pythagorean identity to obtain \(\frac{\sin(\alpha)}{1+\cos(\alpha)}\). The approach to obtain the second formula is similar.
Finally:
$$ \textbf{\textcolor{lightgreen}{Layer 4: Half-Angle Identities}} \\ \begin{align*} \sin^2\left(\frac{\alpha}{2}\right) &= \frac{1 - \cos(\alpha)}{2} \\ \cos^2\left(\frac{\alpha}{2}\right) &= \frac{1 + \cos(\alpha)}{2} \\ \tan\left(\frac{\alpha}{2}\right) &= \frac{\sin(\alpha)}{1 + \cos(\alpha)} \end{align*} $$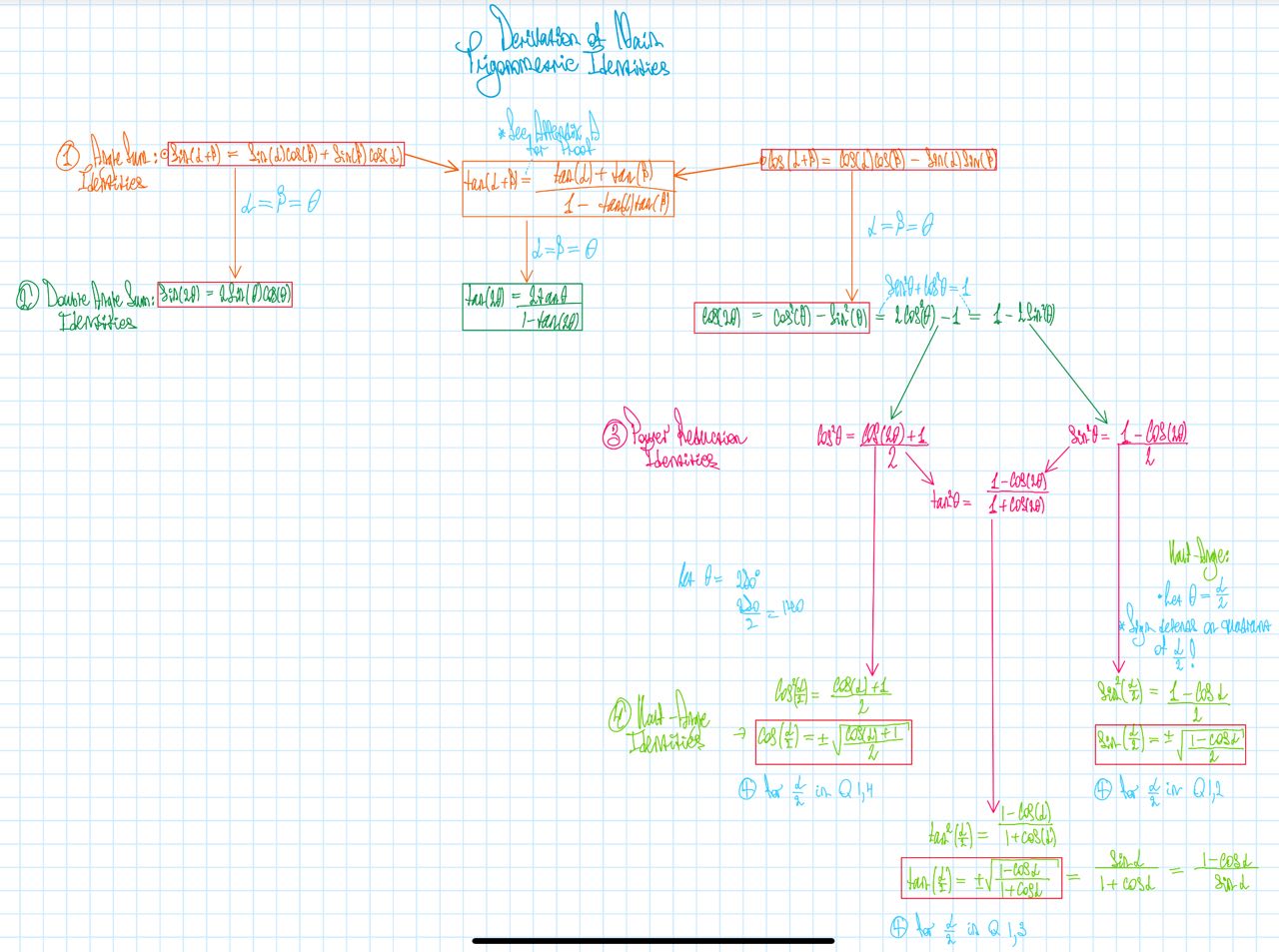
Trigonometric Identities Diagram
Diagram note: Each “layer” of identities is displayed in respective color, with additional explanations in light-blue and key identities enclosed in red rectangles. Zoom in to see in detail.
If you are still in doubt about some steps, refer to ProofWiki for detailed proofs.